In industrial production, there are many rotating objects whose internal temperature needs to be measured and controlled. For example, drying cylinders in the textile industry, rolling mills for rolling mills, rotors for electric machines, and draft heating rolls in the chemical fiber industry. Since the object to be measured is rotating at a high speed, temperature measurement must be performed in a non-contact manner. The platinum thermal resistance and the passive RC network form a sensor that can rotate together with the object to be tested, and the required excitation signal is utilized by magnetic coupling. 3.1 Obtain ωn and calculate the measured temperature T Wire Rope Thimble,Thimble,Stainless Thimble Zhongji Rigging Co., Ltd. , http://www.carbon-steelrigging.com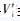
The sensor is sensed contactlessly and becomes the input signal Vi of the passive RC network (see Figure 1). The sensor has a frequency selection function, and the output signal Vo is inductively induced by magnetic coupling to become a feedback signal V'o. Subsequent display controller pair 
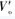The analysis process is performed, and then converted into a corresponding temperature, and compared with a given value, thereby controlling the surface temperature of the object to be tested. 
with 
The relationship 2.1V'i and V'o is the signal ω?n - the carrier of the natural frequency.
The RC passive network using the Wien Bridge is shown in Figure 2. The network has frequency selection characteristics, taking R1=R2=RT (platinum thermal resistance), and its natural frequency ωn is a function of temperature T°C. Obviously, the temperature T and the natural frequency ωn have a one-to-one correspondence. Taking Fn = ωn / 2π, Table 1 describes the relationship (partial data) corresponding to the temperature T and the frequency Fn. T is independent of the size of V'I and V'o. In the information transmission of the entire network, ωn is the information we need, and V'i and V'o are only the carriers of the information.
2.2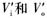 
Quantitative relationship and constraints
Is a sinusoidal excitation signal, ω is its angular frequency, so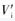 
=Vimsinωt, feedback signal 
. Let the temperature of the measured object be T at a certain time, the resistance value of the corresponding platinum thermal resistance is RT, and the natural frequency of the RC network is ωn=1RTC. Take Vim=8V, when the excitation signal angular frequency ω<ωn or ω>ωn, the measured feedback signal Vom is about 600mV; when the excitation signal angular frequency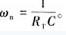 
When Vom has a theoretical value of 0, the actual value is about 30 mV. See Figure 3. 
Theoretically, Vom=0, but V'o is actually measured as an AC signal of several tens of mV in size. The first reason is that in addition to the frequency of ω=ω?n in the excitation signal, there is also the existence of higher harmonics. Higher harmonics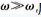 
The second reason is that the presence of the distributed capacitance of the printed circuit causes the excitation signal to be directly coupled to V'o through these distributed capacitances, and Vom is of course not equal to zero. 
Because we do not know the measured temperature T in advance, the ωn of the RC network exists objectively and varies with the change of T. The function of the control unit shown in Fig. 1 is to obtain ωn of the network at this time, thereby displaying the measured temperature T at that moment according to Table 1.
3.2V'i is a sweep signal from small to large
V'i is used as the excitation signal, and the feedback signal is obtained by frequency selection in the RC network.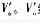 
After rectification, AD conversion is converted to digital quantity V(n). The excitation signal ω is increased by one step to obtain V(n+1), and the ω continues to increase to obtain V(n+2). The MCU system continuously judges, such as V(n), V(n+1) and V(n+2), which are similar in size, indicating that the ω of the excitation signal is not ωn. The excitation signal from the controller is displayed and its ω continues to increase. The system continues to judge the new V(n), V(n+1) and V(n+2), such as once a certain time V(n+1) is much larger than V(n) and V(n+2) are small, then the frequency ω of the excitation signal at time n+1 is stored, because the frequency ω may be the natural frequency ωn of the RC passive network, which contains Temperature information of the measured object.
3.3 Using phase detection to lock ωn
Because the measurement control system is in the factory site, it is subject to various disturbances at all times. The existence of these disturbances often produces an instantaneous minimum value V(n+1) and satisfies the conditions of V(n)V(n+1) and V(n+2)V(n+1) (see Figure 3). This minimum value V(n+1) is false, and its corresponding ω is not the ωn we want, so it must be eliminated. How to tell whether the minimum value V(n+1) is true or false?
Further analysis of the RC passive network of the Wien Bridge, its phase-frequency characteristics (theoretical values) are shown in Figure 4. At ω = ωn, the phase of the feedback signal V'o hops. The actual measurement of the detection system found that its jump is much larger than the theoretical value. We can completely judge the true and false of the minimum value V(n+1) by means of the phase transition characteristics.
Each step of the excitation signal ω is increased as long as the step size is appropriate 
Determine the value of φn+2 minus φn+1, such as →0, then the phase of V(n+1) and V(n+2) does not jump. The value of V(n+1) is small, but it is False, should be removed. If it is large, the phases of V(n), V(n+1), and V(n+2) are hopped, and V(n+1) is the true minimum. At this moment, the ω of V(n+1) is what we want to lock. See Figure 4.
3.4 Summary
Once the microcontroller system detects V(n)V(n+1) and V(n+2)V(n+1); and their corresponding phases are not satisfied: φn≈φn+1≈φn+2, then this is locked. The ω of the time V(n+1) is stored and displayed by the look-up table.
It is not a concept to find a specific phase size or to find the magnitude of a specific phase difference and to determine whether the phase difference is zero (ie, phase difference zero detection). Our system only needs to judge whether the phase has jumped or not, and it can be realized by a phase difference zero detection system. The phase difference detection system can use analog methods, digital methods, or a combination thereof, and will not be described here.